カイ2乗検定をかんたんに把握したいときはないでしょうか。
けど、そんな中で悩むことは、
・カイ2乗検定の具体例で説明してほしいがどこにもない
ですよね。
今回はそんなお悩みを解決する
説明していきます!
もくじ
カイ2乗検定とは?

カイ二乗検定(χ²検定)は統計学でよくでてくるメジャーな方法です。
カイ二乗検定を簡単に言うと、「実際のデータが、期待されるデータとどれだけ違うか」を数値で示す方法となります。
この数値により、二つのことがどれくらい関連しているかどうかの度合いを、
肌感覚ではなく、数字で把握し、他の人に説明ができるようになるといった、優れものというわけです。

説明するときにこのような違いがでます。
・営業トーク「このAとBの関係はものすご~くありますね!」
・アナリスト「このAとBの関係度数は基準が3.8に対してカイ二乗値は約18.2であり、基準値を大幅に超えていますので、統計的に有意な関係があると判断できます。」
説得力がちがいますよね!
カイ2乗の「カイ」とは?
「カイ」(Chi)とは、ギリシャ文字の一つで、大文字では「Χ」、小文字では「χ」と表されます。
カイ二乗検定(Chi-squared test)では、小文字の「χ」カイの二乗値(χ²値)を計算します。
カイ二乗検定では、χ²という記号が使われるのは、検定の基本的な計算式が観測度数と期待度数の差の二乗(つまり、差の平方)に基づいているためです。
そのため、この検定の名前には「二乗」が含まれています。
カイ二乗値が大きい場合、観測データと期待データの間には大きな違いがあることを意味します。
カイ2乗検定のステップ

カイ二乗検定を実施するステップについて簡単に説明します。
- 何を調べるかを決める
例えば、「ある学校の生徒が朝食を食べるかどうか」と「テストの成績が良いかどうか」の関係を調べたいとします。 - データを集める
生徒たちに、朝食を食べるかどうかとテストの成績についてのアンケートを取ります。 - 表を作る
アンケートの結果を、「朝食を食べる」「朝食を食べない」という列と、「成績が良い」「成績が悪い」という行で表にします。 - 期待される数字を計算する
もし朝食と成績に関係がなければ、どのような数字が期待されるか計算します。
例えば、「朝食を食べる」生徒の半分が「成績が良い」と予想されるかもしれません。 - 実際の数字と比較する
実際のアンケート結果と、期待される数字を比較します。大きな違いがあれば、朝食と成績には何らかの関係があるかもしれません。 - カイ二乗値を計算する
この違いの大きさを数値で示すために、カイ二乗値というものを計算します。 - 結果を判断する
カイ二乗値が大きければ大きいほど、朝食と成績には関係がある可能性が高いと考えられます。

カイ二乗値の計算
カイ二乗値の計算はちょっとむずかしいですが、サンプルデータを交えればわかりやすいですのでもうすこしお付き合いください。
カイ二乗値の計算で求めることは上記の通り「実際のデータが、期待されるデータとどれだけ違うか」となり、
具体的には各カテゴリの「実際の観測度数」と「期待される度数」の違いを数値で出していきます。
これは、次の式で計算されます。

「実際の観測度数」と「期待される度数」の内容については次の通りです。
実際の観測度数
- 定義
実際の観測度数は、実験や調査を通じて直接観測された、特定のカテゴリに属するデータの数です。 - 例
例えば、ある学校でスポーツをする生徒としない生徒のテスト成績に関する調査を行ったとします。ここでの実際の観測度数は、「スポーツをする生徒のうち成績が良い人の数」「スポーツをしない生徒のうち成績が良い人の数」など、実際に調査した結果として得られた数字です。
期待される度数
- 定義
期待される度数は、観測データが完全にランダムであるという仮定の下で、理論上期待されるデータの数です。これは、全体の標本の中で特定のカテゴリが発生する確率に基づいて計算されます。 - 計算方法
期待度数は、関連する行と列の合計値を掛け合わせて、全体の標本数で割ることで求められます。
式は次のようになります。
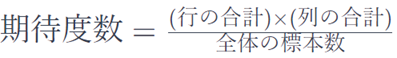
- 例
先ほどの学校の例で言えば、「スポーツをする生徒の総数」と「成績が良い生徒の総数」を掛け合わせ、全体の生徒数で割ることで、「スポーツをする生徒のうち成績が良い生徒の数」の期待度数を計算します。
カイ2乗検定の例

上記で少し触れましたが、「スポーツをする生徒としない生徒のテストの成績に差があるか」という問いを例とし、カイ2乗検定を求めていきます。
サンプルデータとして、スポーツをする生徒としない生徒の数、それぞれの成績についてのデータを用います。
このデータを表にまとめ、期待度数を計算します。
以下のようなデータがあるとしましょう。
スポーツをする生徒の数:100人
スポーツをしない生徒の数:100人
スポーツをする生徒のうちテストの成績が良い人:60人
スポーツをする生徒のうちテストの成績が悪い人:40人
スポーツをしない生徒のうちテストの成績が良い人:30人
スポーツをしない生徒のうちテストの成績が悪い人:70人
これを表にすると以下のようになります。
| 成績が良い | 成績が悪い | 合計 | |
|---|---|---|---|
| スポーツをする | 60 | 40 | 100 |
| スポーツをしない | 30 | 70 | 100 |
| 合計 | 90 | 110 | 200 |
カイ二乗検定の手順
- 期待度数の計算
各セルの期待度数は、対応する行と列の合計の積を全体の合計で割って求めます。
例えば、「スポーツをする生徒で成績が良い」の期待度数は、
(100 × 90) / 200 = 45
となります。 - カイ二乗値の計算
各セルについて、
(実際の度数 - 期待度数)² / 期待度数
の計算を行い、
これらの値の合計を求めます。これがカイ二乗値です。
カイ2乗検定の結果の解釈
計算結果によると、カイ二乗値は約 18.18 です。
この値が大きい場合、実際の度数と期待度数には大きな違いがあると解釈されます。
統計的に有意な差があるかどうかを判断するためには、このカイ二乗値をカイ二乗分布表の臨界値と比較する必要があります。
一般的には、5%の有意水準(p < 0.05)での臨界値を使用します。
この例では、自由度が
(行の数−1)×(列の数−1)=1なので、
自由度1のカイ二乗分布表での臨界値を参照します。
もしカイ二乗値が臨界値よりも大きければ、
スポーツをするかどうかとテストの成績には統計的に有意な関連があると結論付けることができます。
まとめ
今回は、カイ2乗検定を通じて、データ間の関連性を数値で示す方法を学びました。
この手法は統計学の基礎としても重要な概念で、データの解釈に役立ちますので是非身に着けてもらえばと思います。

















コメントを残す